

If the afternoon class has 50% more students, then we could say that the morning class has x students and the afternoon class has 1.5 x students. In fact, if we knew only the average for each group and the fact that the afternoon class had 50% more students, we could again compute the overall average. Note that if we no longer had the individual students’ grades, but only had the class averages and the number of students in each class, we could still find the mean of all the students’ grades, in this way, by finding the weighted mean of the two class averages. Or, we can compute weighted average of the two class means already calculated, using the number of students in each class as the weighting factor: To find that the overall average, we can to total all the grades and divide by the total number of students: However, the average of all the students’ grades is not the average of 80% and 90%. The arithmetic mean of scores in the morning class is 80% and the arithmetic mean of scores in the afternoon class is 90%. The grades in each class on a particular test were: Let’s say we have two classes, one with 20 students, and one with 30 students. These weighting factors allow us to count some values as “more important” in finding the final value than others. When totaling the individual values, each is multiplied by a weighting factor, and the total is then divided by the sum of all the weighting factors. The weighted average is similar to the arithmetic mean. Understanding weighted averages will help you solve some GMAT questions that specifically deal with an arithmetic mean and also some probability questions. So we divide 319 by 28 to get the mean age: To compute the arithmetic mean of the children’s ages, we find the sum of the ages in years for this class, which is 319. If a question concerns the arithmetic mean, it will generally use the phrase “average (arithmetic mean).” This average is the sum of all values divided by the number of values:Ĭonsider the data in the table and histogram above.


No GMAT question will ever refer to simply an “average,” leaving you to guess what it’s talking about. To find the median, we generally have to put the elements of the set in order first – and count them, if we don’t know the number of elements in the set. Both of these values are 11, so the median of the children’s ages is 11. This is an even number of values, so the median will be the average of the middle two values–the 14th and the 15th values. There is always one median for a group of numbers.įor example, consider the data in the table and histogram. If the number of numbers is even, then the average of the two middle points is the median. If the number of numbers is odd, the median is the middle ranking score. To find the median of a set of numbers, rank the numbers. The median is the middle value in the data set. A list of numbers may have more than one mode. Here there are two modes: 11 years and 12 years. Suppose that we tally the age to the nearest whole year of a class of children and we get the following result: A mode is similar to a plurality in an election or vote the candidate who gets the plurality or most votes wins in a certain election format, even he or she doesn’t get the majority (over half) of the votes. The mode is the value with the highest frequency count.įor example, if there are seven 12-year olds in a class, ten 13-year olds, and four 14-year olds, the mode is 13, since there are more 13 year olds than any other age.
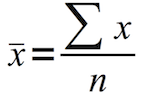
If we go through a data set and tick off once each occurrence of a particular value, we obtain the frequency count for the data. The mode is the most frequently occurring value in the data. We’ll start with a discussion of the mode. The descriptive statistics most commonly tested on the GMAT are the three main types of average, more formally known as “measures of central tendency”: the arithmetic mean or common average, the median, and the mode. In other words, you have a group of numbers, and the statistics tell us about that group – what the values are clustered around or how tightly they are clustered, for example. Averages: Arithmetic Mean (Average), Median, and Modeĭescriptive statistics are measures of a population or data set.


 0 kommentar(er)
0 kommentar(er)
